確実性等価キャッシュフロー（CEQ）法の計算例

前回は確実性等価キャッシュフロー（CEQ）による評価法のシンプルな例について解説しました。ここで、もう一度公式を掲載しておきます。

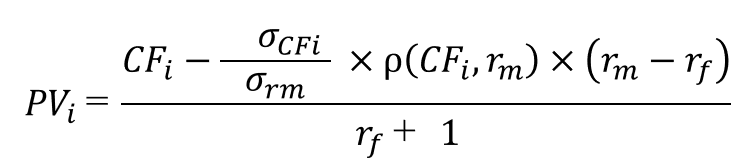
ここではより実務に即した形で評価を行っていきたいと思います。ここでは主に2つの方法でこの評価をしていきます。まずは、 モンテカルロ法（Monte Carlo Method） を用いた方法、次にシナリオ分析を用いた方法です。モンテカルロ法を用いた手法は少し難しい部分もありますので、その場合は2番目に挙げるシナリオ分析の解説をご参照ください。シナリオ分析を用いる方法は容易に実行できるでしょう。

評価自体は、以下に挙げた前提条件に加えて、「期待FCF」と「FCFの標準偏差」という2つの材料があればCEQ法における「計算」はできます。モンテカルロ法でもシナリオ分析でもあくまでその大きな違いはこの2つの指標を得るためのアプローチの違いです。

なお、本事例における評価にあたっては、この会社は負債のない会社であること、基本となる プロジェクション（Projection） は既に作成してあること、不確実な変数が複数存在することを前提として行ってみたいと思います。なお、負債のある会社で、負債の簿価が市場価値と見做せる場合には、FCFからは負債の返済額も控除してFCFE（株主に帰属するキャッシュフロー）に変換して評価します。

また、計算の前提として、以下の数値を仮定します。

市場リターンの標準偏差：　σrm＝20%
リスクフリーレート：　rf＝1%
マーケットリスクプレミアム：　rm－rf＝7%
対象銘柄リターンと市場リターンの相関係数：　ρ＝0.3

 

モンテカルロ法を用いたCEQ法による評価

モンテカルロ法によるFCF分布の取得

 

まず、本書で説明したような「プロジェクション」が既に策定済みであることを前提としています。今回は本書で解説したプロジェクションとはまた異なるプロジェクションを用いて評価を行っています。今回例示する会社は事業部が3つ存在し、3つの事業部があるという前提をおいています。プロジェクションの策定にあたっては、それぞれの事業部毎にKPIを置いて評価しています。ここで、特にA事業部については顧客増加率（年次、%）、B事業部については大口顧客数（年次、社数）、C事業部については顧客増加率（年次、％）に不確実性があると考えているものとしましょう。そして実際に著者の手元のプロジェクションでもこの3つの変数の値を変えると異なる結果が計算されるようになっています。

この場合、この3つの変数を不確実な変数と見做して評価していきます。例えば、A事業部においては顧客増加率の初期値（つまり前年度から今年度までの増加率）を年間20%として考えました。ここで関係者間で「この20%という顧客増加率はまだまだ伸びる、ただ不確実だ」と予測しているとします。

１．「大体20%という顧客増加率が今後5年間でどのくらいの比率で上昇していくのか」という点
→ここで、「ざっくり5%くらいは伸びそうだ」と考えたとします。この場合、この5%は「成長率の伸びる比率」ですから、来年の顧客増加率は20%×（１＋5%)＝21%になると予測していることになります。この「基本的な成長率」である「5%」をよく「ドリフト」といいます。

２．「顧客増加率の基本的な成長率がそのまま（つまりドリフト＝0%）だとして、そのブレ（リスク）のみを考えたときに、そのブレ幅（リスク）はどの程度だろうか」という点
→これこそが標準偏差の考え方です。標準偏差は、ネットで検索すればわかりますが「期待値の＋－１標準偏差の間に約68%の確率で値が分布する」という性質を持ちます。このため、もし「期待値が変わらず20%で、およそ68%位の確率で24%～16%くらいの範囲に分布するだろう」と考えられるとすれば、「額」でみた標準偏差は「4%」となり、「比率」でみた標準偏差は「20%」になります。

「額」でみた、「比率」でみた・・・というのが少しわかり辛いかもしれませんが、こう置き換えると理解できるでしょう。例えば、顧客増加率を株価だと考え、20%や4%という数値を100倍して20円や4円だと仮定しましょう。この場合、基本的な成長率は0%とすれば、現在株価20円、1年後の期待株価は20円、ただし1年後の株価は期待株価を中心に24円～16円の間に68%の確率で株価が分布するということになります。このため、「額」でみるとと4円が標準偏差ですが、比率でみるとその4円を現在株価を分母にしたスケールでみると4円/20円＝20%ということになります。

よく株式について「期待収益率（期待リターン）」や「収益率の標準偏差」を尺度に CAPM（資本資産評価モデル） 等色々な計算を行いますが、モンテカルロ・シミュレーションで用いた株価モデルでも、標準偏差は「比率（株式であれば収益率）」ベースのものを用います。このため、上記の１と２を併せて考えた場合、顧客増加率は「ドリフトは5%、比率でみた標準偏差は20%であることから、現在値が20%であれば、1年後の期待値は21%で、68%の確率で25%～17%に分布する」と考えることができます。

このような前提で、モンテカルロ・シミュレーションを行ってみました。その結果が以下の図及び表です。なお、このモンテカルロ・シミュレーションは、現実の確率測度（リスク中立ではない）のもとで、さきに挙げた3つの変数を不確実な要素と捉え、それら各変数に対して上で説明したとおり「基本となる成長率（ドリフト）」と「標準偏差」の仮定値をおき、その上で正規乱数を使って不確実性を作り出し、それぞれの要素を1年毎に予測し、それら変数をプロジェクションに入力することでFCFを計算する・・・という過程を1,000回繰り返したものです。

実際の計算に用いたモデルは、「％」で表される指標に対しては「一般化ウィナー仮定」というモデルを少し改良したモデル（結果が正規分布に従う）を用いてシミュレーションし、「社数」で表される確率以外の指標に対しては本書P335で解説したモデル（結果が対数正規分布に従う）を使ってシミュレーションしています。これらのモデルについてはブラックショールズモデルとも関係するので、必要に応じて関連書籍を読んでいただくと良いでしょう。このあたりのことは市販の書籍では解説が難しいものが多いので、時期をみてまた噛み砕いた形で解説したいと思います。

さて、以下の図は著者のPC上のモンテカルロ・シミュレーションの結果です。最終年度の標準偏差が大きな値となっており、厳密には少し問題があるのですが、そこは考えずに説明を続けます。

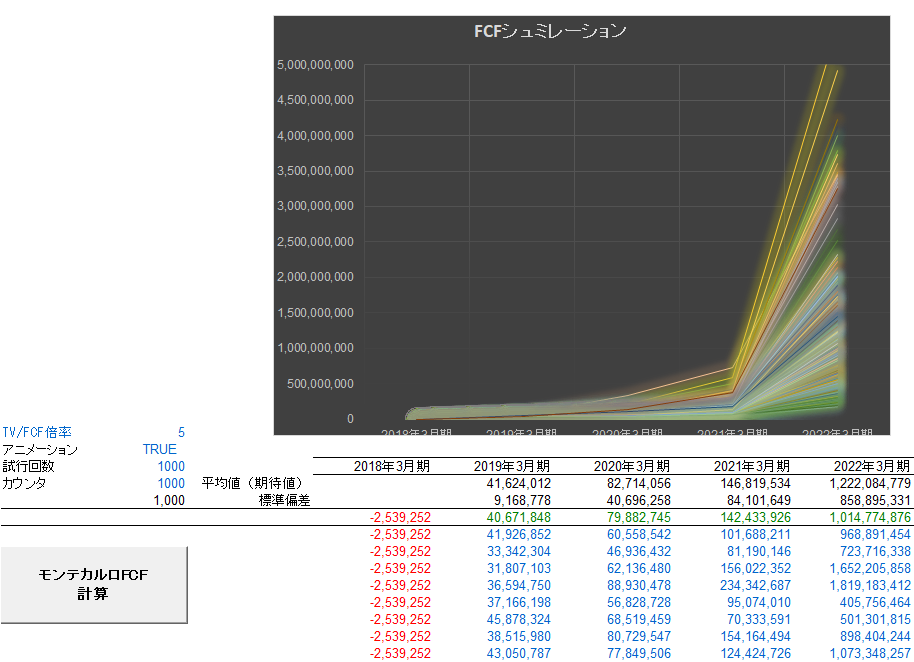
上の折れ線グラフが、各変数をモデルを用いて4年分シミュレーションし、その値を用いてプロジェクションを再計算し、そのプロジェクションからFCFを算出する・・・という過程を1,000回のシミュレーションしたものです。そのすぐ下に、「平均値（期待値）」という行がありますが、これが1,000回シミュレーションを実行した際の各予測年（今回は4年間予測している）の平均FCFです。これこそが期待FCFといえるものです。このモデルでは4年後の2022年3月期末に会社を売却したものと想定し、通常のFCFに加えてさらにFCFの5年分のFCFが追加して期待できるものとの仮定をおいており、このため2022年3月期の期待FCFだけが大きな値となっています。なお、上図では最終年度の売却額を含めたFCFが50億円を超えるようなシナリオも存在していることがわかりますが、平均的な値は「平均値（期待値）」に記載の1,222,084,779となっています。なお、このシミュレーションを実際に確認し50億円を超えるシナリオの数を数えたところ1,000回中6回のみでした。

さらに下には「標準偏差」という行がありますが、これが1,000回シミュレーションを試行した場合の各年のFCFの「金額ベース」の標準偏差です。標準偏差の定義どおり、約68%の確率で平均値からー1標準偏差～＋1標準偏差の間にCFが分布することを意味します。例えば、2022年3月期であれば、期待FCFが1,222,084,779、標準偏差が858,895,331であることから、1,000回のシミュレーションのうち、およそ680回程度が363,189,448～2,080,980,110の間の数値となるであろうということを意味します。

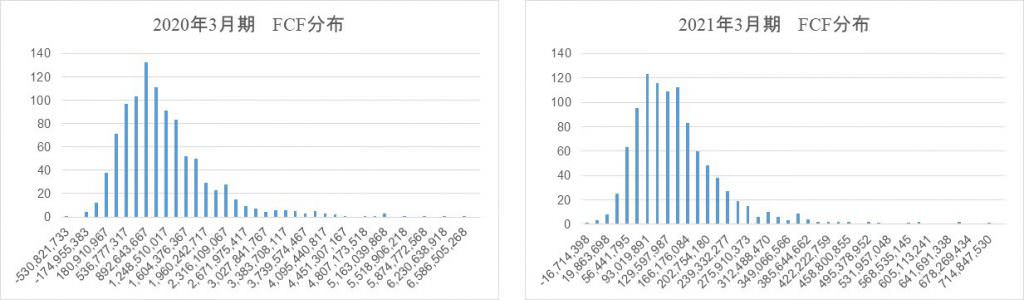
また、念のため分布形状を確認するため、ここでは2020年3月期のFCFと2021年3月期のFCFにかかるヒストグラムを作成しました。以下に見て取れるように、モデルの前提どおりおおまかに対数正規分布に従っていることがわかります。

ここまでくれば、あとは公式に当てはめるだけでCEQにおける評価が可能となります。

 

モンテカルロ法の結果を用いた実際の評価

 

まず結果から先に見てみましょう。以下がモンテカルロ・シミュレーションを用いたFCFとFCFのリスク（標準偏差）を材料にCEQ法の考え方で評価した結果です。
評価結果は32行目です。この数値は30行目の数値を合計した数値となっています。

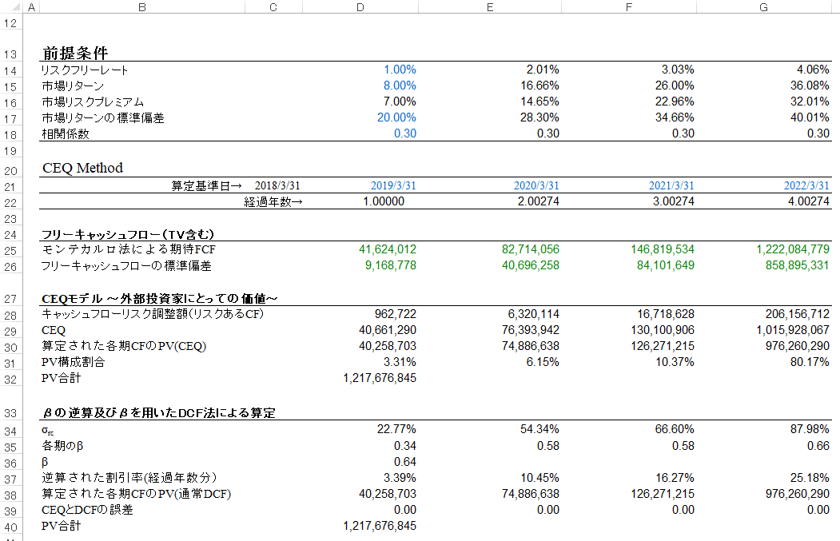
CEQ法では、通常の エンタープライズDCF法（Enterprise Discounted Cash Flow Model） のように期待FCF自体をβから求められた割引率を用いて（1+r）のn乗で割引く・・・という計算をするわけではなく、各期のFCFのうちリスクのあるCF分を控除する作業が発生します。このとき、「リスクあるCF」の計算には、上式のとおりFCFの標準偏差、市場リターンの標準偏差、相関係数、 マーケットリスクプレミアム（MRP） が必要となります。このとき、例えば、2年後のFCFを評価する場合、相関係数をひとまず所与とすれば、FCFの標準偏差は単純に観測値から計算できますが、市場リターンの標準偏差とマーケットリスクプレミアムは2年換算の数値を用いねばなりません。このため、これらのデータについては便宜上、1年換算のものから4年換算のものまで計算をしていいます。通常のDCFでは期待FCFを（1＋rf）のn乗で割り引けば計算できますが、CEQ法ではリスクあるCFの計算をしなければならず、その過程の中で算定日から割引時点までの期間を考慮する必要があるのです。

例えば4年間換算の市場リスクプレミアムは32.01%と計算されています。この計算は4年換算の市場リターンと4年換算の リスクフリーレート（Risk Free Rate） の差として計算します。4年換算の市場リターンは（1＋8%）の1461／365乗から1を引いたものとなります。簡単にやろうと思えば単純に4年なので「4乗」でもいいのですが、ここではうるう年も考慮して1461／365＝4.00274という指数を使っています。4年換算のリスクフリーレートも同様に（１＋1%）の4.00274乗から1を引いたものとなります。このように、各前提指標については、評価対象年から評価日までの年換算の期間に相当する値を用いることが重要となります。通常のエンタープライズDCF法であれば割引時に期間を考慮するだけで一気に現在価値を計算できますが、本手法の場合は割引処理時のみならず、リスクあるCFを計算する過程でも期間を考慮した比率を用いる必要があるという点には注意が必要です。

関連して、分かりにくいであろうと思われる部分のみセルの計算式を以下に記載します。

2年目のリスクフリーレート（E14セル）
=(1+$D14)^E$22-1

2年目の市場リターンの標準偏差（E17セル）
=$D$17*SQRT(E22)
※リターンの標準偏差は、期間ではなく期間の平方根に比例して増大することからこの計算となる。

2年目のキャッシュフローリスク調整額（リスクあるCF）（E28セル)
=(E26/E17)*E18*E16

2年目の算定された各期CFのPV（CEQ）（E30セル）
=E29/(1+$D$14)^E22

また、本モデルでは逆算的にβの算定を行い、またそこから経過年数分の割引率（1年換算ではない）を求め（37行目）、そこからDCF法的に価値を算定しても結果としてのPV評価額が同じになる（32行目と40行目）ことを示しています。また、β値は0.64と逆算されていますが、これも類似会社から取得するβとしてはよくある数値となっていることがわかります。

 

シナリオ分析を用いたCEQ法による評価

 

CEQ法ではより簡易的にシナリオ分析を用いた評価も可能です。簡易的と表現していますが、むしろモンテカルロのような複雑なことをやるよりもこちらの方が有用かもしれません。例えば、以下のような3つのシナリオを考えます。こういったシナリオを準備し、おおよそこの3つのシナリオで対象事業の将来の大枠がつかめるということになれば、細かいことを無視すれば、ここで計算された期待値と標準偏差を用いてCEQ法により対象会社の評価を行うことも可能となります。この手法を行う場合、割引率の要素の一部でかつ捉えにくい部分といえる「対象会社キャッシュフローの不確実性」をより明確に示す形で評価できることになり、合理的に相関係数さえ決定できれば通常の類似会社βを用いたエンタープライズDCF法より根拠の示しやすい状態で評価ができるともいえます。

また、この手法の場合、M&Aの売却者と買収者の方で前提条件の考え方さえ合意形成してしまえば、ざっくりとしたお互いの将来に対するリスクを含めた考え方も内包された形で評価結果を確認できることになります。例えば、両当事者で「2019年3月期のFCFは25%の確率で60百万、50%の確率で41百万、25%の確率で38百万になるだろう」といった合意ができれば、この数値だけで期待FCFと標準偏差が求められるので、標準偏差＝変動の程度＝リスクも含めて評価できることになります。

参考までに、2019年3月期の期待値及びFCFの標準偏差のセルに挿入している式を以下に記載します。

期待値（D7セル）
=D3*$C$3+D4*$C$4+D5*$C$5

FCFの標準偏差（D8セル）
=SQRT((D3-D7)^2*$C$3+(D4-D7)^2*$C$4+(D5-D7)^2*$C$5)

このシナリオ分析を用いたCEQ法による具体的評価は「ENTREPRENEURIAL FINANCE（2011年、著者Janet Kiholm Smith, Richard L. Smith, Richard T.Bliss)」のChapter 10にて具体的な事例を用いた解説があります。ご関心あられる方は参照してみると良いでしょう。

また、これは両手法ともにいえることですが、本手法を用いるにはいくつかの注意点があります。相関係数はどういった値を用いるべきか、どの程度の標準偏差の範囲であれば合理性を持つのか等いくつかの論点があります（ただ、著者による調査では、相関係数はこれら文献で説明されているより日本の場合はより高いように思います）。本サイトでの解説はあくまでも評価手法の「紹介」にフォーカスを当てていますので、実際の評価にあたっては「ENTREPRENEURIAL FINANCE（2011年、Janet Kiholm Smith, Richard L. Smith, Richard T.Bliss)」のChapter 10や「Principles of Corporate Finance（Brealey,Myers,Allen）」等にて具体的な解説がありますので、そちらを参考にすると良いでしょう。