確実性等価キャッシュフロー（CEQ）法の考え方

本書ではベンチャー企業評価に向く手法として、 CAPM（資本資産評価モデル） を数式変換して、分子を確実性等価キャッシュフロー（無リスクキャッシュフロー）にしてから評価する 確実性等価キャッシュフロー法（CEQ法） について述べました。ここでは実際の M&A 現場レベルの算定作業を行ってみたいと思います。本書ではCAPMを数式変換すると以下のような式となることについて、ページを割いて解説しました。しかし、実際の算定については本書では触れていませんでした。ここでは実際の算定について考えてみたいと思います。

CEQ法における算定式

本書の解説にとおり、CAPMモデルをPV＝の形で変形して表現すると以下の通りとなります。この変形には本書で解説したとおり、CAPMモデルをCFやPVを用いた表現に変換し、分散や相関係数の性質等を利用して以下のように数式変換するものでした。

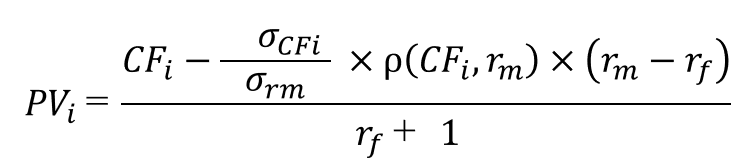
これを用いて、実際に算定を行ってみましょう。

 

CEQ法による評価　～シンプルなケース～

 

まず、非常にシンプルに以下の変数を当てはめて、ある会社の期待CFの現在価値を評価してみましょう。

1年後の期待CF	800
市場リターンの標準偏差	20%
CFの標準偏差	300
CFと市場リターンの相関係数	0.4
市場リターン	8%
リスクフリーレート	1%
マーケットリスクプレミアム（8%－1%）	7%

これによると、分子は以下のとおりとなります。

800－（300／20%）×0.4×7%＝758

上記を、分母にあるとおり、リスクフリーレートで割引くと以下のとおりとなります。

758／1.01≒750.495

これがCEQ法による現在価値の算出方法です。さて、逆にこの結果から割引率とβを逆算してみましょう。この場合、まず割引率を算出します。割引率は以下のように求められます。これは単純に「割引き」の反対のことをしただけです。

800／750.5－1≒6.5963%

この場合、CAPM式より、以下の数式が成り立ちます（CAPMの式は本書を参考としていただくかネットで検索して調べていただければと思います）。

6.5963%＝1%＋β×7%
β＝（6.5963%－1%）／7%＝5.5963%／7%＝0.7994

さて、この場合、対象会社CFを「収益率」でみた場合の標準偏差をみていきましょう。β＝0.7994ということは、求めたい標準偏差を「x」とおくと、以下のように算出できることになります。βを意味する数式は「市場と個別銘柄のリターンの共分散」を「市場リターンの分散」で除して求める方法と、「対象資産リターンとマーケットリターンのリスクの比」に「市場と個別銘柄リターンの相関係数」を乗じる方法の二通りの表現が良くされますが（結果は当然同じ）、以下の式は後者の式を使っています。

β＝0.7994＝x／20%×0.4
∴　x＝0.8／0.4×20%＝39.9736%

これが対象会社CFを「収益率」でみた場合の標準偏差ということになります。さきほど、現在価値が750.495でしたから、収益率の標準偏差である39.9736%を、金額ベースであるCF標準偏差に変換して300となるか念のため確認してみましょう。以下のように確認すると、CFで見た標準偏差に一致することがわかります。

750.495×39.9736% ≒ 300　※小数点以下の取扱により手計算では少しずれます

本書でも述べた通り、この手法の良い点は、類似会社βを用いるのではなく、対象会社のCF計画やその予測されたボラティリティ（標準偏差）から価値を求めることができる点です。

次回はより複雑な実務的なケースについて評価をしてみたいと思います。