期待FCF
期待FCF(期待フリーキャッシュフロー)とは、全ての資金提供者(株主や債権者等)へ帰属する期待値的なキャッシュフローを意味し、標準的な エンタープライズDCF法(Enterprise Discounted Cash Flow Model) における割引対象の利益指標として採用されます。
期待FCFは成功した場合に予想される将来の「(成功時の)予測FCF」とは異なります。簡潔に言えば、ある対象会社に無限回の未来があった場合に、それぞれのFCFをその発生確率で加重平均した期待値的なFCFを意味します。より詳しく説明すると、次の図中の太線で示したFCF計画こそが「期待FCF」です。
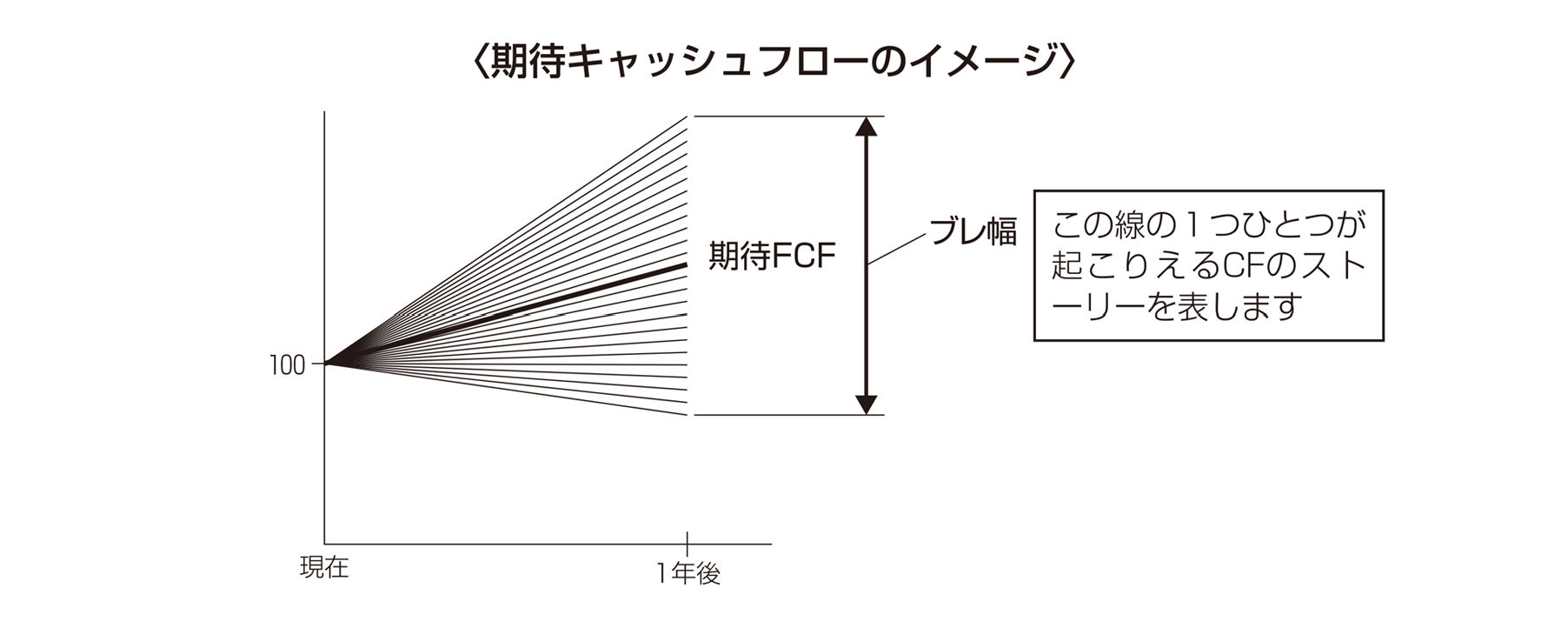
期待キャッシュフローを用いるべき理由
DCF法で割引対象となるFCFに「期待値」的なキャッシュフローを用いなければならないのは、「資本コストで割り引くから」です。これは、次の図をみていただくとよりわかりやすいと思います。
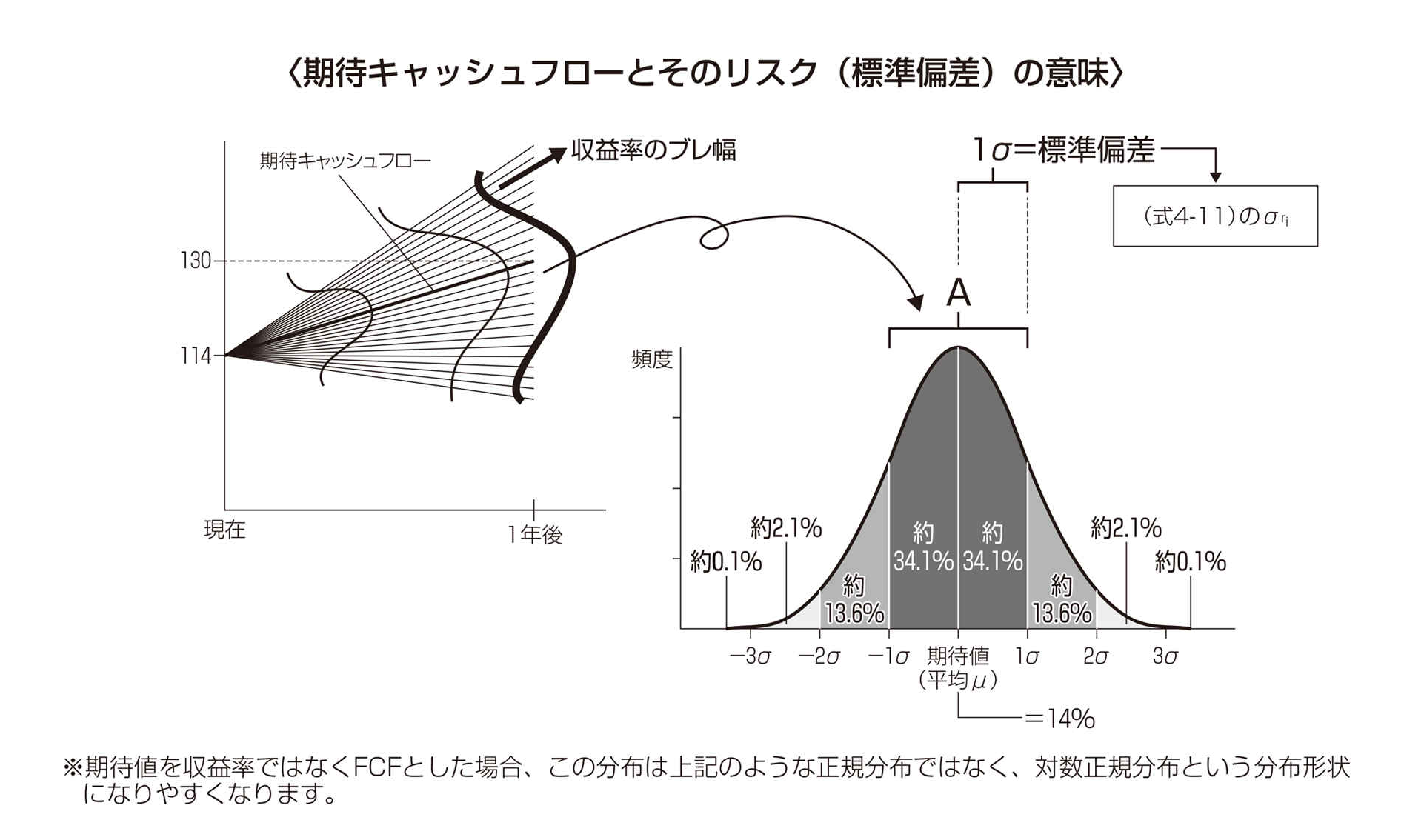
左側の図は、考えられる1年後のキャッシュフローストーリーを線で表現したものです。
この中の太線で示した部分こそが「期待FCF」ですが、ここで1年後の期待FCFを130と仮定しましょう。
現時点における株式の買収額が114円と1年後の売却額が130円であると考えれば、 期待収益率(期待リターン) が約14%となります。もし1年後の130という期待FCFを割り引こうとするならば、(借入がない会社であれば)その割引率は「株主資本コスト」です。
株主資本コストの最も重要な材料の1つは「収益率」のブレ幅から求められる「標準偏差」です(前掲の図参照)。このブレ幅を図中に表現したものが、期待キャッシュフローを中心として被さっている釣鐘状の太い曲線です。この太い曲線を90度左に回転させ、「頻度」を縦軸に、ストーリーの広がりを「横軸」にして描いたのが右側の図です。
これは期待収益率を平均(μ)、(期待収益率の)標準偏差を1σとした正規分布です。正規分布は自然科学の様々な場面で観測されるもので、平均値の付近にデータが集積するような確率分布のことですが、 CAPM(資本資産評価モデル) は収益率がこのような分布に従うものと仮定して理論が構築されています。
正規分布や標準偏差についてすでにご存知であればご理解いただけると思いますが、期待収益率が14%、標準偏差である1σが20%であれば、「実際の収益率は、約68%の確率で期待収益率14%の上下20%である『約-6%~+34%』の範囲(つまり図のAの部分。-1σ~+1σ)に収まるであろう」ということを意味します。
なお、同図に記載しているとおり「約-26%~+54%」(-2σ~+2σ)の範囲に約95%の確率でなることを意味するというのも、標準偏差と正規分布の基礎理論のとおりです。ちなみに、この釣鐘状の曲線内の面積の合計は1(=100%)となります。
なぜ期待FCFをβを材料とした割引率で割り引くのか? ~βの基本式~
期待FCFと標準偏差の考え方がわかれば、次に標準偏差と割引率の関係性についての理解が重要になります。ある対象会社株式の収益率の標準偏差が大きいということは、期待収益率を中心とした実際の収益率のバラつき(リスク)が大きいことを意味します。
現代ポートフォリオ理論では投資家が危険回避型の思考を有しており、リスクが大きければそれに応じた高いリターンを要求するという前提が置かれます。この前提を数式として表現したものがCAPMであり、そのリスクの度合いともいえる指標こそがβです。
以下の(式4-10)~(式4-12)は表現を変えてβを表現したもので、ともに同じことを意味します。(式4-11)をみれば明らかなとおり、対象会社株式の収益率の標準偏差「」が上昇すれば、それに応じてβが上昇し、CAPMで算定される資本コスト(割引率)も上昇することがわかります。このことをβの基本式をみながらより深くみていきましょう。
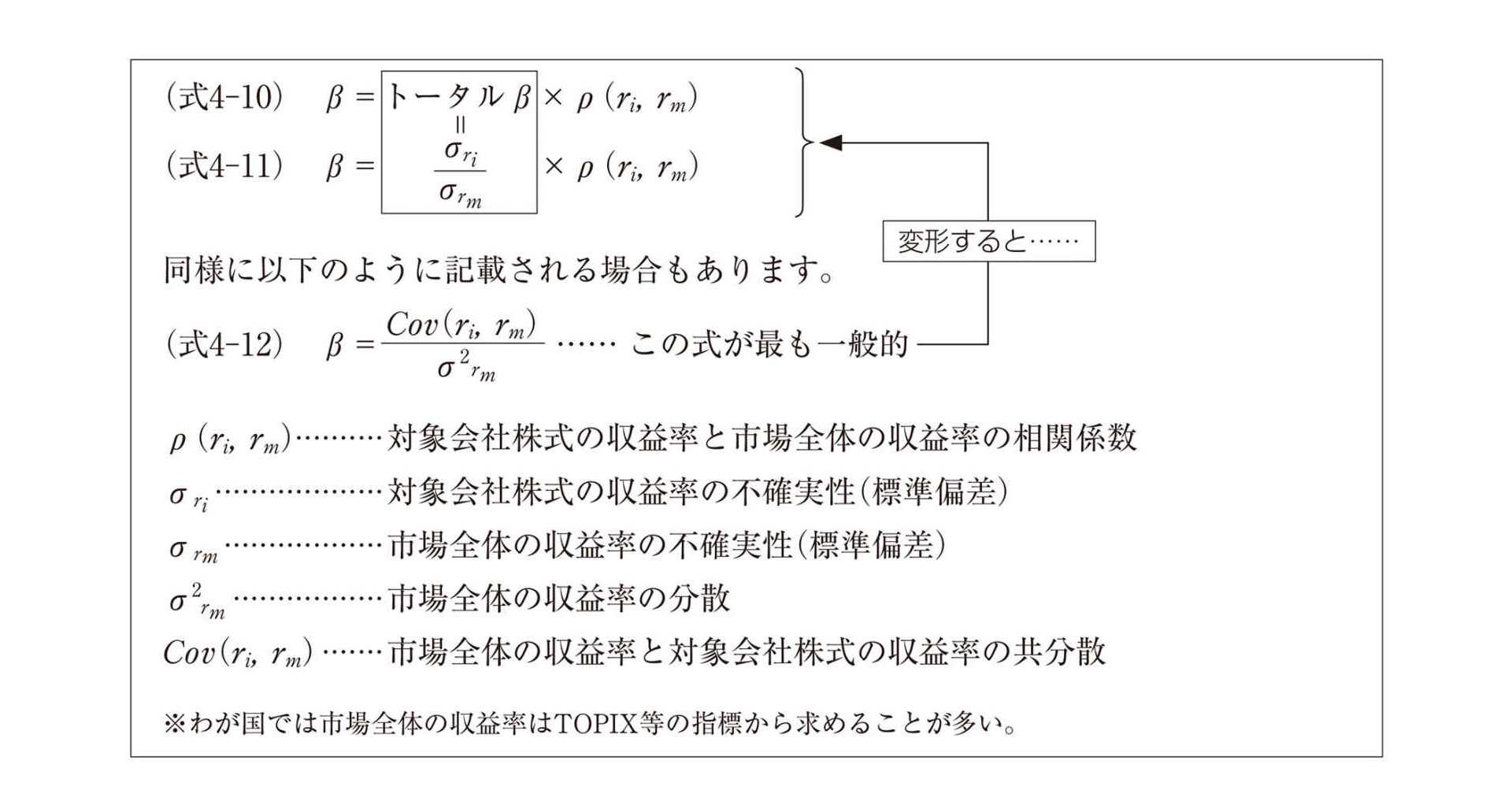
対象会社株式の収益率の標準偏差を株式市場全体の収益率の標準偏差で除すことで算出できる「トータルβ」は、本来はまだ通常のDCF法に用いる(式4-10)~(式4-12)の左辺で表された「β」ではありません。
なぜなら、ファイナンス理論では、標準偏差で表されるその会社の「総リスク」や、「総リスク」を基準として算出されたリスク倍率である「トータルβ」は、投資家が分散投資を行うことで相当程度減殺され、下方修正されるという考え方をとるからです。
この「分散投資によるリスク減殺効果」を調整する項が、上式「ρ(ri,rm)」という項であり、「トータルβ」に乗じられることで通常のDCF法で用いる「β」が算出されていることがわかります。
この「ρ(「ロー」と読む)」は対象会社株式の収益率と株式市場全体の収益率の連動性を意味する相関係数を意味します。この相関係数が低ければ、その対象株式に投資するトータルリスクが減るというのがβ計算における考え方です。
この相関係数は、多くの市場データに鑑みると0.1〜0.7程度をとることが多いようです。つまり、投資対象となる対象会社、株式収益率と株式市場全体の収益率の相関が低ければ低いほど、「トータルβ」からリスクが大きく減殺され「β」は低い値となります(ただし、βの説明力は減る)。
ベンチャー企業等では「総リスク」である標準偏差が非常に大きく、相関係数が小さいという組み合わせとなるケースが多く、実はそれほど大きな「β」にならないという指摘もあります。
このあたりは少し難しい内容なので、興味のある方はこちらのコラムも併せてご覧ください。
もちろん、相関係数ρによりリスク減殺がされるとしても、β算出の根本ともいえるのは対象会社の収益率の「総リスク」を意味する上式の「ρ ri」です。この「総リスク」についてより深く考えていきましょう。
前掲の図では「ρ ri」を「対象会社株式の収益率の不確実性(標準偏差)」と定義しました。これは、投資の文脈でいえば「投資による収益率(=売却額/投資額-1)の不確実性」と同義です(ただし、投資額=現在価値)。
また、たとえば、無借金会社である対象会社の現在価値が100、期待収益率が10%、期待収益率の不確実性(標準偏差)が5%だと考えれば、1年後の将来価値=期待FCFは110、FCFベースの標準偏差は5となります。
FCFの不確実性の5という数値は、収益率ベースでみた不確実性である5%に現在価値を乗じた「金額ベース」の不確実性に他なりません。このことから、「ρ ri」は、「期待FCFの不確実性を比率で表現したもの」であるともいえます。
したがって、DCF法において期待FCFを割り引く場合、本来はまさにその期待FCFの不確実性を比率で表したものである「ρ ri」を主要材料にβを求め、そこから求められた資本コストで割り引いているという一貫性があるのです(実務ではβを他社データから推定することもあるが)。
つまり、期待FCFをそれ自体の不確実性を適切に織り込んだ割引率で割り引くのです。投資家が危険回避型の思考を有する大前提の中では、FCFのリスク=不確実性が大きければ大きいほど、将来の期待FCFと比較してその期待FCFの現在価値を低く見積もらねばならないということになります。
これは同時に、期待FCFではなく大成功した場合のFCFをCAPMにて導かれた割引率を用いて割り引くことが誤りであるということでもあります。CAPMの主要材料であるβは、期待収益率を中心とした正規分布を前提に、個別銘柄と市場全体のリスク倍率を主な材料の1つとして用いて算出された値です。
また割引率算定上の相場的な基準値ともいえるリスクプレミアムも期待値の性質を有します。よって相場として用いるリスクプレミアムが期待値的性質をもつとすれば、算定された割引率も期待値的な値となり、評価対象のFCFに期待値でない適当な基準のFCFを用いて割り引いても論理的な整合性がとれないのです。
以上のような背景があるため、DCF法を行う際には プロジェクション(Projection) の策定において複数のストーリーを策定し、期待値的なプロジェクションを検討することが有効なのです。
プロジェクションを慎重に策定していけば、どの要素の不確実性が高く、どの要素の不確実性が低いかということはある程度理解できるようになります。この場合、不確実性が高いものについて複数のシナリオを準備して各シナリオに発生確率のウエイトを付し(合計が100%になるように)、そのうえで各シナリオで算出されたFCFを加重平均することで「不確実性」を考慮に入れた「期待FCF」を算出するということもできます。
