βの推計と相関係数、分散投資効果について 2

前の記事では「不確実性（リスク）が高い場合は割引率も高くなる方向に影響する」ということが、相関係数が高い場合に分かりやすく理解できるという説明をしました。なぜなら、相関係数が低い場合は、トータルリスク（個別銘柄の標準偏差／市場指数の標準偏差）が打ち消されることから、個別銘柄の標準偏差が相対的に高いからといってβが高くならないからです。

 

ここでβの考え方をもう一度整理してみたいと思います。前記事でも申し上げたとおり、βという指標もリスクを表します。しかし、βリスクは単純にその投資対象の標準偏差（リターンのブレ）だけでなく、分散投資を十分にしている投資家からみたその投資対象のリスクを計測したものといえます。

βの考え方の整理

ここまで見てきてわかることは、投資家が持っているポートフォリオが市場指数と個別銘柄である場合、その個別銘柄のリスクが同じであっても、この2つの相関係数が低ければ低いほど、その2つを適当な組み入れ比率で組み入れを行った場合のポートフォリオのリスクは、効率的な組み合わせにすればするほど低減されるということでした。

 

逆に、相関係数が高ければ高いほど、如何に効率的な組み合わせにしてもリスクの低減効果が働かないといえます（というか効率的な組み合わせがない）。またβはこの分散投資によるリスク低減効果を考慮にいれた指標であるということも理解いただけるでしょう。ここまでわかってはじめて、以下の疑問に回答することができます。

 

• βにはなぜ分散投資によるリスク低減効果が含まれているといえるのか、すなわち、なぜ「システマティックリスク」のみが反映されているといえるのか？

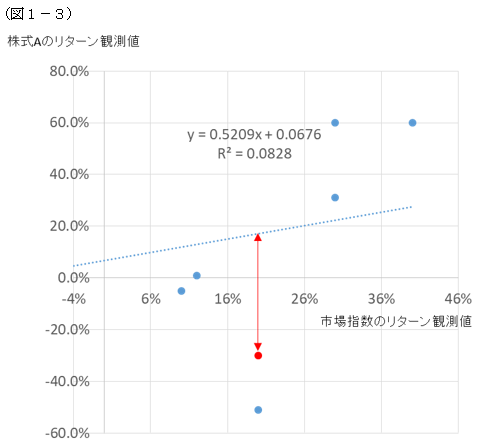
（図１－３）や（図１－４）で描いた線分の意味をもう少し深くひも解いていきましょう。以下に（図１－３）と（表１－５）を再掲します。

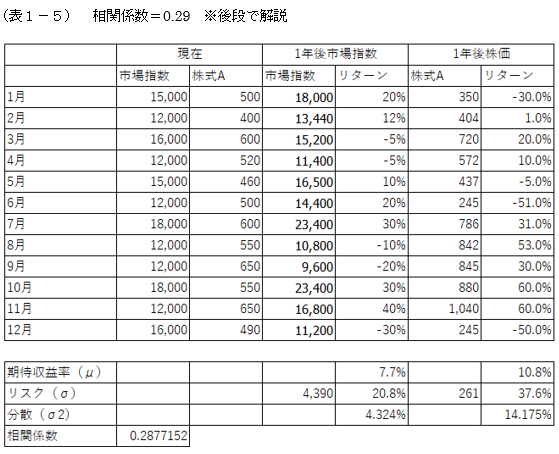
※ここでは、分散の計算材料として用いた「リターン」を%表記のまま、つまり30%であれば「0.3」として用いています。一方、多くの書籍では、おそらく、10%や20%などという数値を「10」「20」に置き換えて計算しており、面倒ですが、そのほうが分散＞標準偏差となり分かりやすいです。例えば、リターンが20%なら「20」、-30%なら「-30」と%を省いた数値を用いて分散を計算していくと、分散としては約432という結果が出ます。これに％を後付けするわけです。しかし、√4.324%も20.8%、√432に%を付した数値も20.8%と同じ値となり標準偏差では変わらないため、標準偏差が正しければよいと考えてこう計算にしています。

 

この線分はよく見ていくと「市場ポートフォリオのリターンと切片のみがわかれば個別銘柄のリターンが決定される」という式になっていることがわかります。よく見ると切片は「定数」なので、「変数」は市場ポートフォリオのリターンのみです。これはつまり、市場ポートフォリオのリターンのみが個別銘柄のリターンを決める変数となっている関数であるということになります。

 

βが表現する「システマティックリスク」の定義は「市場リターンの変動に対応するリスク」であり個別リスクは含まれないリスクです。この定義どおり、この関数式で表現される個別銘柄のリターンは「市場リターン（の変動）」という変数のみにより決定されることとなります。さて、それではなぜ、投資家が被るリスクについては、このようなリスク指標で考えてよいということになるのでしょうか？

 

まず「トータルリスク」と「分散投資によりリスク低減効果を考慮した後のリスク」を比較してみることから説明をしていきましょう。（図１－３）で示した相関係数が約0.29の事例を見ていきましょう。まず、個別銘柄のリスク（トータルリスク）と市場指数のリスクは（表１－５）より、それぞれ37.6%、20.8%という数値が出てきます。また、市場指数リスクに対する個別銘柄（トータルリスク）の単純なリスク比率は個別銘柄リスク／市場指数リスクでみると、37.6%／20.8%＝1.807倍という形で表現できます。

 

本書で「トータルβ」と表現した値がこの値です。一方、市場リターンの変動のみで個別銘柄の変動を図ろうとした場合のリスク比率はβで表現されることから、そのリスク比率は（図１－３）の傾きより0.5209倍となっています。このため、個別リスク（トータルリスク）がどの程度減少したのかを考えるには、個別リスク×0.5209／1.807で測れそうです。これを計算すると、37.6%×0.5209／1.807＝約11%となります。

 

この約11%という数値が、トータルリスクである37.6%に含まれるシステマティックリスク部分であるということができます。つまり、ここで示した市場指数と株式Aのポートフォリオを組むことにより、株式Aのリスクが37.6%からあたかも約11%に下がったように考えることができるというのがβの考え方ということになります。このリスクの減少分をよく見てみると、0.5209／1.807＝約0.29ということになり、まさに相関係数を乗じた分だけリスク減少しているといえます。つまり、株式Aのシステマティックリスクは以下のように計算できるともいえることになります。

 

 

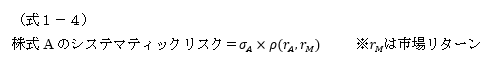
また、同じように考えると、同時に市場指数のシステマティックリスクは以下のように定義できます。

 

 

市場指数に新たに投資しようという投資家がすでに十分な分散投資をしているとすれば、その新たな投資対象である市場指数と既にその投資家が投資しているポートフォリオは実質的には同じリスク・リターンを持つと考えることができることから、（式１－５）内の相関係数は、「自身との相関」ということになり必ず「1」となるため、σMが市場指数に投資する場合のシステマティックリスクであるということがいえます。より正確には、市場指数の場合、システマティックリスク＝アンシステマティックリスクであるともいえます。

 

ここでβの式を意味する（式１－３）を再掲します。

 

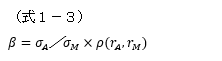
これを見ると、（式１－３）で示されるβの式は、実は（式１－４）を（式１－５）で除した値となることがわかります。つまり、βとは、市場指数のシステマティックリスクに対して、個別銘柄のシステマティックリスクがどの程度大きいのか？という比較だということになるのです。

分散投資をすればアンシステマティックが消えるとはどういうことか？

これまでみてきたように、βの考え方は個別銘柄と市場指数のシステマティックリスクの比較指標と考えてよいということでした。しかし、本当にアンシステマティックリスクが分散投資により消えるという仮定は成り立つのでしょうか？また、ポートフォリオをどの程度組めばアンシステマティックリスクが十分に低減されるといえるのでしょうか？

 

これについては、1980年代のデータですが、 Meir Statmanという学者の研究「How Many Stocks Make a Diversified Portfolio?」では、およそ30～40のポートフォリオを組むことで、ほぼアンシステマティックリスクがなくなるという結論となっています。以下の表を見ればそのイメージがつかめると思います。およそ10の銘柄を組み入れることで、一つの銘柄のリスクが約50%削減され、75銘柄を組み入れることで約60%削減され、それ以上は組み入れ銘柄数を増加させてもそれほどリスクが削減されないという結果になっています。

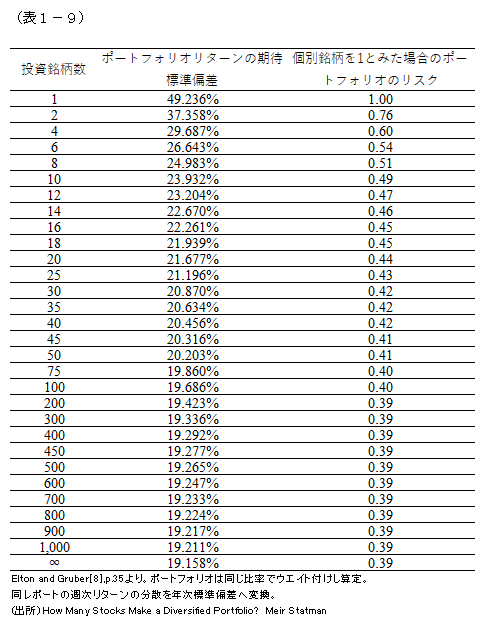
βの考え方は、このように十分な分散投資をしている投資家を前提としているわけです。そうすると、このような例えば上記表でいうところの既に100の銘柄に投資をしているような投資家からみれば、そこに1つの銘柄を加えたところで「市場リスク」に伴って増減するようなリスクを除く個別リスクであるアンシステマティックリスクはほぼ消えてしまうと考えることができるようになります。言い換えると、上のように市場の平均的なリスクに収れんしていくという言い方の方が正しいかもしれません。

 

こうなると逆に、「市場リターンの変動に連動して動く個別銘柄のリターン変動部分」は逆に「無視できないもの」ということになります。なぜなら、当然のことながら、分散投資をして平均的なリスクに近づいたとしても、その平均的リスクともいえる市場リターンの変動に連動して動く個別銘柄の変動については消去できないからです。

 

全ての銘柄のリターンには、このような「市場リターンの変動に連動して動く個別銘柄リターン変動部分」が原則的には含まれます。このため、十分に分散投資が行われたポートフォリオにおいては、個別銘柄のそれぞれが「市場リターンの変動に連動して動く個別銘柄のリターン変動部分がどの程度か？」によってポートフォリオ全体のリスク・リターンが定まります。

 

当然、市場にある全ての投資銘柄に投資をしてしまえば、結局は市場リターン・市場リスクに一致するポートフォリオとなります。しかし、そうでない場合は、次に投資する銘柄が、どの程度の「市場リターンの変動に連動して動く個別銘柄のリターン変動部分」を持つかにより、次の投資銘柄を組み入れた後のポートフォリオのリスクが変わってくるのです。

 

このように、分散投資をし、殆どのアンシステマティックを認識しない状態になった投資家としては、「自身が持つポートフォリオに対して新しく投資する銘柄がどの程度そのポートフォリオ全体のリスク上昇・下落に寄与するか」を見ていくことが重要となり、その際の関心の矛先こそがシステマティックリスクなのです。

 

そして、その寄与度を考える際には、自身が持つポートフォリオと新たな銘柄の「関係性」、つまり「相関係数」や「共分散」が重要となります。それにより、システマティックリスクが大きく変わってくるからです。ここで、前記事の冒頭で説明した図をもう一度見てみましょう。

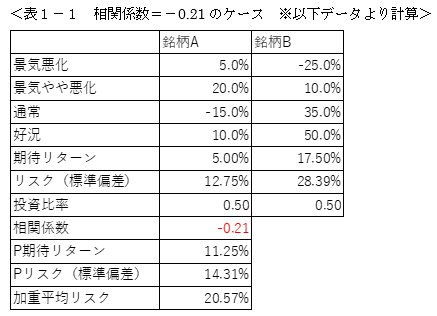
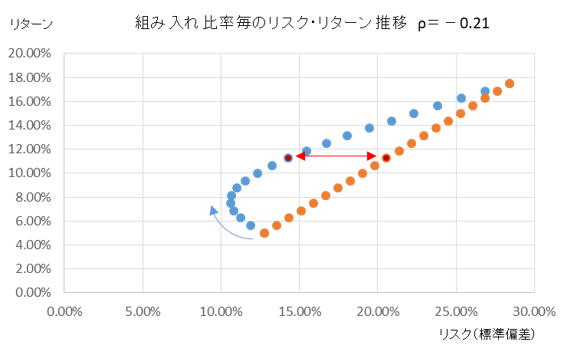
ここで、仮に銘柄Bというものを、ある投資家が既に投資しているポートフォリオだと考えましょう。また、銘柄Aというのが新たに投資を考えている銘柄だと考えましょう。銘柄Aを企業価値評価の対象となる株式と考えても良いでしょう。この場合、銘柄B＝分散投資ポートフォリオだと考えると、既に十分に分散投資を行っている投資家からみると、単純に銘柄Aの標準偏差が高いからとって、銘柄Aに対する投資リスクが大きいとは判断しません。

 

なぜなら、前記事での解説のとおり、銘柄Aと既存の投資ポートフォリオ（＝銘柄B）の相関係数が低ければ低いほど、上図のようにポートフォリオを組んだ場合にリスクが低減すると考えることができるからです。赤い横矢印の長さがポートフォリオを組むことによるリスク低減効果であることは前記事で説明したとおりです。

 

ここまでの説明で、なぜβにより分散投資をしている投資家にとってのリスクが測れるのかについてイメージはつかめて頂けたと思います。

アンシステマティックを図で理解する

それでは、アンシステマティックリスクは先ほどの（図１－３）や（図１－４）において、どこに表れているのでしょうか？（図１－３）をもう一度見ていきましょう。

これは、正確な表現ではありませんが、図中の線分から、それぞれの月の株式Aのリターンを表す各点までの距離（縦の長さ）がそのイメージに該当する部分といえるでしょう。例えば、（図１－３）の赤い縦矢印で示した部分です。よく見てみると、相関係数が高い場合はこの高さが小さい点が多く、相関係数が低い場合はこの高さが大きい点が多いことが見て取れると思います。

 

正確な定義ではありませんが、この高さというのが「アンシステマティックリスク」と同じような概念であるともいえ市場リターンを尺度として計れない変動ということになります。しかし、先の説明のとおり、相当数の投資をしている投資家から見れば、様々な投資銘柄がこの赤い縦矢印のようなリスクを相殺し合い（つまりある銘柄はそれを表す点が線分より上にあり、またある銘柄はそれを表す点が線分の下にあるような状況）、結局はこの青い線分で示すような市場リターンの変動に伴う個別銘柄の変動の関係性のみが重要な関心事となります。

分散投資をしていない投資家からみるとどうなるか？

前述のとおり、十分に分散投資をしている投資家を前提とすれば、次の投資案件も既存のポートフォリオと組み合わせればアンシステマティックリスクは消えると考えてよいから、システマティックリスクでみた場合のリスクのみが興味の対象となります。しかし、分散投資していない投資家からみると話が変わります。以下に再掲する（式１－１）のブルー部分に含まれる相関係数や共分散の項目でリスク低減が図れないからです。これは実際に数字を入れてみればよく分かります。

（式１－１）により、全資産を銘柄Aに投資している投資家を考えます。この場合WAが「1」となり、WBは「0」になります。この場合、（式１－１）のブルー部分は「0」となり、またグリーン部分も「0」となることから、この投資家から見たポートフォリオのリスク（標準偏差）は単純にσAとなります。一つの銘柄しか投資をしていないのでポートフォリオとは本来は言えませんが、相関関係の低い2銘柄以上の場合と比べて、単純にリスク低減が図れないことはご理解いただけると思います。

 

ここで銘柄Bがβの話で言うところの分散投資ポートフォリオまたは市場指数だとしましょう。こう考えると、この投資家は、分散投資ポートフォリオを持たずに銘柄Aのみに投資をする投資家であると考えることができます。βの考え方では、ここでいう銘柄Bのような市場ポートフォリオに十分に投資をしている投資家からみたリスクを考えますが、この投資家は銘柄Bには一切投資をしていません。このため、上式でいうところのブルー部分に該当するようなリスク低減が図れないのです。このため、通常のβの考え方ではリスクを計測することはできず、アンシステマティックリスクを含めたトータルリスクを受けることになります。

 

上では、1銘柄への投資は本来ポートフォリオとはいいませんが、WBを「0」とおいてポートフォリオの計算に当てはめて「ポートフォリオのリスク」を計算しました。これはβという値の性質に照らして理解を深めていただきたかったからです。前述のとおりβとは「自身が持つポートフォリオに対して新しく投資する銘柄がどの程度そのポートフォリオ全体のリスク上昇・下落に寄与するか」という指標ともいえます。

 

つまり、投資家が既に保有する投資ポートフォリオがない場合においては、分散投資によりリスク低減効果が図れないので「新しい銘柄のリスクの全部がポートフォリオ全体のリスク上昇に寄与する」ということになることわかると思います。

 

別の言い方をすれば、銘柄Aのみに全財産を投資する投資家は、「銘柄A＝ポートフォリオの全部」ということになり、銘柄Aでみてもポートフォリオでみてもリスクは同じになるということでもあります。それゆえ、銘柄Aのリスクは、そのリスクがそのままポートフォリオのリスクに寄与するということになるのです。

 

これは、（表１－９）の投資銘柄数1の場合と同じです。このような分散投資をしていない投資家は、既存のポートフォリオと組み合わせることでリスク低減が図れないことから、（式１－４）のようなシステマティックリスクに相当するリスク（分散投資によりリスク低減が図れた前提で認識されるリスク）ではなく、トータルリスクであるσAをリスクとして認識すべきということになります。

 

したがって、このような投資家にとってのβを考える場合、（式１－３）のρの項目を取った（またはρ＝１として、リスク低減効果が働かないと仮定した）βを考えるべきということになるのです。これがトータルβの考え方です。ただし、「投資」にも「競合」がつきものです。

 

このため、仮に自身が分散投資していない投資家であり、認識するリスクが大きいからといって、特定の投資案件に対して高い要求収益率（低い投資時Valuation）を求めるということはできません。そうしてしまうと他に十分に分散投資を行っている投資家が多いこの世の中においては、他の投資家に投資案件を取られてしまうことになります。こういったことを考慮すると、十分に分散投資をしている投資家が多いこの世界においてはβでリスクを図ろうということになるのです。